Written by: Heather Ferris – An experienced Las Vegas blackjack dealer.
Ever since Edward Thorpe exposed the game in 1962, Blackjack has increased in popularity as a game of cat-and-mouse. Thorpe’s basic strategy, as well as his Ten Count system, was what pushed that pebble over the hill creating this huge snowball effect of card counting that we know today. Players have numerous systems to choose from and which one you adopt depends on what you’re trying to accomplish. The Hi-Lo count is an easy strategy to learn; is recommended for most situations and will be the system we will be focusing on in this article.
Step 1: Assigning Card Value
The first step to learning the Hi-Lo count is to assign value to the cards. Each card has a specific value that must be memorized. All ten value cards including the Jack, Queen and King, plus the Ace are all valued as negative one (-1). Sevens, eights and nines are valued as zero, or even and twos, threes, fours, fives and sixes are valued as one (+1). By valuing the cards in this manner it makes card counting much easier and obtainable for the average person.

Blackjack Card Counting Values
Homework 1: Identify Card Value
Many hours of at-home practice are required when learning how to count cards. The first homework assignment is to be able to quickly identify the card value without any hesitation. Take a single deck of cards and run through it until you’ve correctly identified the value given to each individual card. For example, when using the Hi-Lo system, if you see a Jack then the correct answer would be Negative One (-1). Keep practicing until you’ve run through an entire deck without making a mistake. This is also a good warm-up exercise to use before card counting.

Identifying Card Counting Values
Step 2: Counting Cards
Now that you know the value of the cards it’s time to count them. It’s better to start the count after the dealer has shuffled the deck and a new round begins. Card counting is not the same as memorizing the deck. The player is mentally keeping track of the ratio of high to low cards. The player will start at zero and add or subtract the value of the card as they are seen there by creating a tally or a running count of the deck. If the count is high, the remaining deck will have a lot of 10’s in it making the situation more favorable for the player. If the count is low, the remaining deck will have more numbers in it making the situation more favorable for the casino.

Running Count while playing blackjack
Homework 2/3: Learn to keep a running Count Of Cards
The second homework assignment is to be able to accurately keep a Running Count of the cards. With a single deck in hand, start at zero and total the values of the cards. You know you’ve succeeded if you hit zero or Even by the end of the deck. If you can do this 9 out of 10 decks then you’re ready to move on.
The third homework assignment is the same as the second however instead of counting one card at a time, now count two. A good card counter will count down a single deck in 20 seconds with one error or less.

Starting a running count

Ending a running count
Step 3: True Count
Now that we can count the cards, what do we do with this information? A count system provides three critical pieces of data. When to bet more, when to deviate from basic strategy and when to take insurance. When making a wager or deciding whether to take insurance professional card counters convert the running count into the True Count. The true count is the actual count or value of the deck when the player is making a decision. You’ll need to convert your running count into a true count on all multi-deck games. However, single deck games will always give you a true count. In order to calculate the true count the player would need to divide the running count by the number of decks remaining. For example, if the running count is +9 and there are 3 decks remaining then the true count is +3. +9 divided by 3 is +3. If the running count is +8 and there are 2 decks left then the true count is +4.

True Count formula
Homework 4/5: Estimate Decks Left & Calculating True Count
The fourth homework assignment is to be able to accurately recognize how many decks are left in the shoe and to use that information to calculate the true count. Buy a shoe and several decks of cards. Place one deck in the shoe in order to get a feel for what that looks like. Then increase it to two. Keep repeating this step until you’ve seen all 8 decks. Complete this exercise several times until you feel comfortable identifying the number of decks in a shoe. In order to test your knowledge, ask a friend to set up the shoe, then enter the room and try to correctly identify how many decks are in the shoe.
The fifth homework assignment is to be able to successfully calculate the true count using your newfound skill. A good way to practice this is to ask that same friend to come back and deal a mock game of blackjack for you. Calculate the true odds in your head and then check the deck and use a calculator to verify if you’re correct.

True Count example with 2 decks
Step 4: Deviations or Indices
Typically, the house edge for blackjack is roughly around 0.5% however it is possible to bring that number all the way down to Even or 0% if Edward Thorpe’s basic strategy is used. That’s why it’s incredibly important to know blackjack strategy by heart. This guide tells players what actions to take during specific situations. We’ve provided several blackjack strategy charts for single deck, double deck and multi-deck shoes as well as for games where surrender is available. Card counters will follow basic strategy the majority of the time. In order to achieve an advantage over the house, counters must know when to deviate from basic strategy. These deviations, or indices, must be memorized and used according to the true count. We have provided a simple chart outlining these indices. This chart will tell you when to deviate from basic strategy. For example, when looking at the cross sections for TT vs. 6 we see +4. This means when the true count is greater than +4 the player will deviate from basic strategy by splitting instead of standing. If we go to 13 vs. 2 we see -1. This means when the true count is less than -1 the player will deviate from basic strategy by hitting instead of standing.
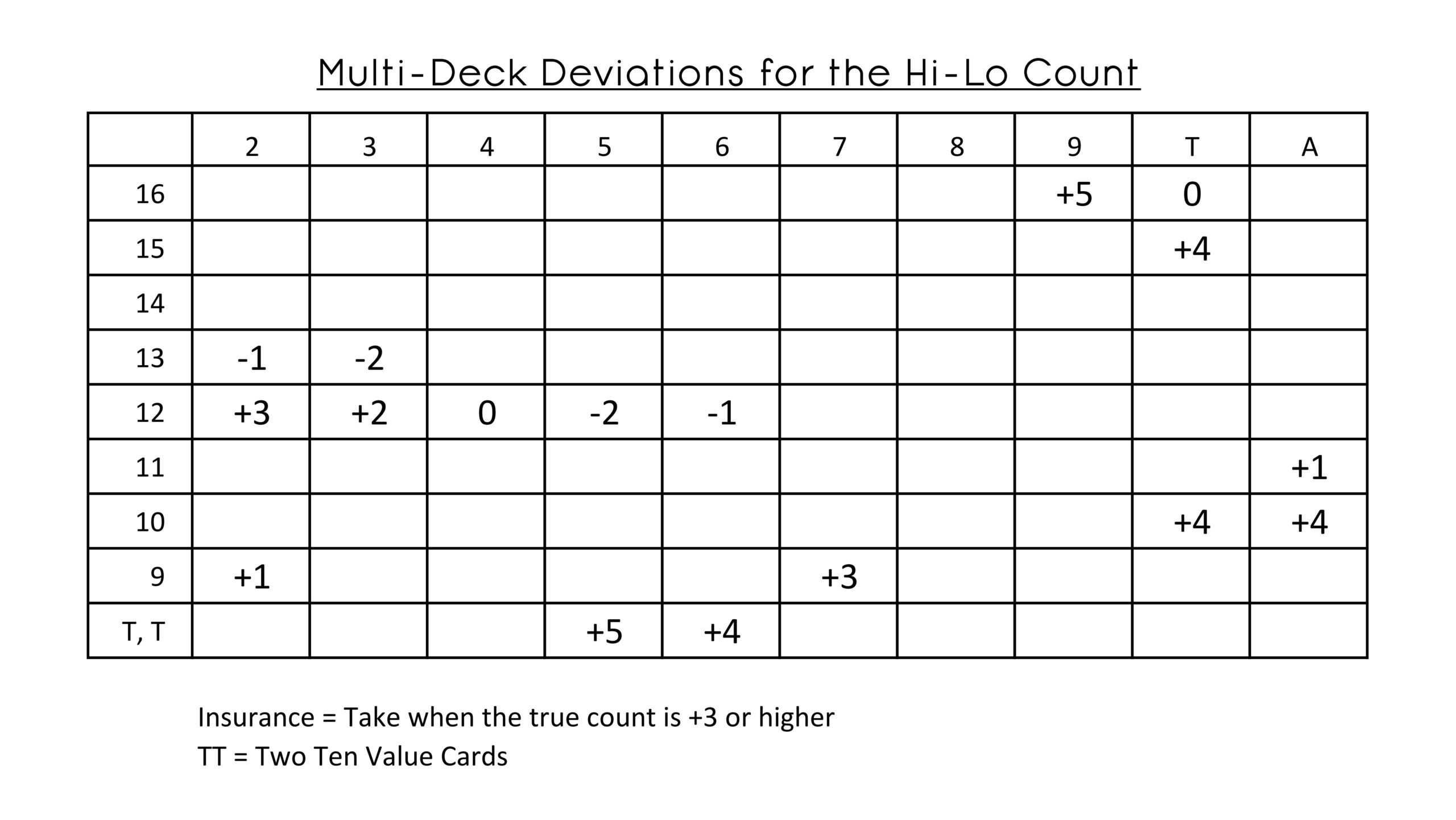 Examples of Basic Strategy Deviations for card counting with Hi-Lo count
Examples of Basic Strategy Deviations for card counting with Hi-Lo count
Blackjack Strategy Cards:
- 4 to 8 Deck Shoe, Dealer Hits on a Soft 17, Surrender is Available
- 4 t0 8 Deck Shoe, Dealer Stays on a Soft 17
- 4 to 8 Deck Shoe, Dealer Stays on a Soft 17, Surrender is Available
- Double Deck Shoe, Dealer Stays on Soft 17
- Double Deck Shoe, Dealer Hits on Soft 17
- Single Deck, Dealer Hits on Soft 17
- Single Deck, Stays on Soft 17
Homework 6/7: Memorize Basic Strategy & Deviations from the Indices Chart
The sixth homework assignment is to memorize basic strategy. You can learn via the classic techniques or, depending on your learning style, you can learn by simulating a hand of blackjack with a deck of cards. This may be more helpful to some people rather than writing the answers down on a sheet of paper. You know how you learn so do what is most comfortable for you. Either way the blackjack strategy should be practiced until it can be recalled instantaneously. The seventh homework assignment is to memorize all of the deviations from the indices chart provided. Create home-made flash cards, writing out the same chart over and over again until it is memorized. These are all classic techniques that will help with learning these deviations. If possible, have a friend deal you a mock blackjack game as you use your newly acquired skills.
Step 5: Bet Spreads
Bet spreads and bankroll requirements are two more tools that are critical to a card counters’ success. Bet spreads is when the player raises or lowers their bet based on the count. A small spread would be 2 to 4 units while a large spread would be 8 to 16 units. Card counters raise their wager when the true count is positive and lower their bet when the true count is negative. Bet spreads are mainly used on multi-deck games and are not typically used on single-deck games. A large bankroll is also needed in order to weather any losing streaks. If the player spreads between $100 and $300 then a bankroll of $20,000 will be needed. If they spread between $5 and $10 then a $2,000 bankroll will be needed. As you can see, with the amount of time, effort and cash investment needed this can quickly become a serious hobby. Card counting can increase the excitement of blackjack as players have fun testing their skills against the house.
Additional Card Counting Methods
Here is a quick overview of popular blackjack card counting methods. There are options for both the beginner and the advanced player.
Hi/Lo Count – This is our recommended card counting system outlined above which gives you many of the advantages of other counting methods without the steep learning curve.
Hi Opt 1 System – This was developed by Charles Einstein in 1968. This is similar to the Hi / Lo System except that 2s and aces are assigned a 0. This makes the system more accurate, but at the cost of being more difficult because you need to keep an ace side count.
Hi Opt 2 System – This adaption of the Hi Opt 1 System was created by Lance Humble in the 70s. It’s more accurate than it’s predecessor, but it’s even more difficult because you need to keep a side count for 8s and 9s, too. That’s on top of needing to keep a true count (for multiple decks).
KO System – This system was developed by Ken Fuchs and Olaf Vancura in 1998. The KO is considered an unbalanced system, because +1s are assigned to 7s, making the overall count end at +4 when you go through an entire deck (instead of 0).
Uston Advanced Count – This system was developed by Ken Uston. It’s considered one of the most accurate card counting systems, but also one of the most difficult to learn and use. The UAC assigns a -1, 0, +1, +2, or +3 to each card. You also need to keep a side count for aces.
Zen Count – The Zen Count was created by Arnold Snyder. This balanced system assigns -2, -1, 0, +1 and +2 to each card. You will also need to figure the true count (before betting). You can learn more about the Zen Count on the Blackjack Forum, or in the book, Blackbelt in Blackjack.
Omega II Count – This was first published in Blackjack for Blood, written by Bryce Carlson. Players will want to figure out the true count, but keeping a side count isn’t necessary (but it is more accurate). This system assigns the values -1, 0, +1 and +2 to each card.
10-Count – The 10-Count was created by Edward Thorp. No one uses it anymore, but that doesn’t make it ineffective. Thorp tested it in Vegas and won more than $11,000 in a weekend. It paved the way for the systems used today, too.
Wong Halves Count – This was created by Stanford Wong, and was first introduced in his book, Professional Blackjack. It is a difficult, yet accurate system to learn and use. This system assigns -1, 0, +0.5, +1 and +1.5 to each card. You also need to figure the true count.
Red 7 Count – This system was developed by Arnold Snyder. Players will need to keep an Initial Running Count (IRC), which starts with -2 for every deck in the game. For example, one deck would be -2, 4 decks would be -8, etc. Then you start counting from there. You can learn more about this system in Blackbelt in Blackjack.

